Here is the project:
http://pre-apcalculusw2.obrienfamily.sent.com/Q4%20Project.pdf
Wednesday, May 26, 2010
Tuesday, May 11, 2010
Miles Last Scribe Post, May 11
We began class with the quiz. It focused mostly on the law of cosines and vectors. We then checked the O'Brien answers to the quiz. We were reminded that the unit test will take place next tuesday the 18th. We then went into vector projection. Tricky stuff to be sure. There were properties and such. A good derivation for Dot Products can be found at:
He fired up his trusty TI-84 Plus Silver Edition. With a flurry of button pushing, he proved beyond a shadow a doubt that theta does, in fact, equal 75 degrees. He then noted that cleverness was a key prerequisite to succes on the unit test. Bad news for Tyler.
Did you ever want to find the projection of vector u onto vector v? Well wait no longer True Believer, the magic formula, for the vector projection of vector u on vector v is: 
Ta-Da!
See you next time Dan and O'Brien.
Friday, May 7, 2010
Scribe Post May 7
warm up:
1.
use applet to show:
a) <3,2> + <2,4>
b)<3,2> + <-5,1>
2.
Do p. 457/70
1.
We plugged in the two coordinates for each problem into the applet, and we added them together (found the sum). We observed the movements of the vectors and concluded that...
(vector between two terminal points of two vectors = Terminal - Initial)
A+(-B) = A-B
B-A=-(A-B)
v=i+2j = <1,0> + 2<1,0> = <1,2>
w=2i-j = <2,-1>
for the homework quiz on Monday we must remember:
we reviewed homework problems, and learned that when
the magnitude of the vector sum must be 3. This is because the magnitude of cos60º and sin60º is 1. The coefficient of 3 then changes the magnitude's value to 3.
73:
<300,0>
" class="ee_img tr_noresize" eeimg="1" style="vertical-align: middle;">
" class="ee_img tr_noresize" eeimg="1" style="vertical-align: middle;">
to find the vector of A+B use...
because you have found the parallelogram created by the vectors of <300,0> and" class="ee_img tr_noresize" eeimg="1" style="vertical-align: middle;"> . knowing that one side of the parallelogram is 300 and the other is 125 use the given formula above to find the vector/resultant of "x".
Dot Product Notes:
if u= and v= then 
=u1(v1)+u2(v2)
ex/ u=<3,4> v=<-2,7>
=3(-2)+4.7
=-6+28
=22
p. 460/ 5 properties:
1.
=
2.
3.
4.
5.
all variables above are vectors other than: all c's and last "o" in property 2
however, when you "dot" the vectors together your product is a scalar.
definition of "dotted products": take two components multiply them together and then add them
scalar is a real number = 17
vector is a directed line segment = ------>
1st Cool Result:
where theta is the angle between u and v
if = 1, vectors in same direction = parallel
if = -1, vectors in opposite direction = parallel
if = 0, vectors are perpendicular = orthogonal
orthogonal = perpendicular
2nd cool result:
the projection of u onto v (see u, in applet) is given by:
this 2nd cool result will be in class discussion on Tuesday
1.
use applet to show:
a) <3,2> + <2,4>
b)<3,2> + <-5,1>
2.
Do p. 457/70
1.
We plugged in the two coordinates for each problem into the applet, and we added them together (found the sum). We observed the movements of the vectors and concluded that...
(vector between two terminal points of two vectors = Terminal - Initial)
A+(-B) = A-B
B-A=-(A-B)
v=i+2j = <1,0> + 2<1,0> = <1,2>
w=2i-j = <2,-1>
for the homework quiz on Monday we must remember:
we reviewed homework problems, and learned that when
73:
<300,0>
to find the vector of A+B use...
because you have found the parallelogram created by the vectors of <300,0> and
Dot Product Notes:
if u=
ex/ u=<3,4> v=<-2,7>
=22
p. 460/ 5 properties:
1.
2.
3.
4.
5.
all variables above are vectors other than: all c's and last "o" in property 2
however, when you "dot" the vectors together your product is a scalar.
definition of "dotted products": take two components multiply them together and then add them
scalar is a real number = 17
vector is a directed line segment = ------>
1st Cool Result:
where theta is the angle between u and v
if
if
if
orthogonal = perpendicular
2nd cool result:
the projection of u onto v (see u, in applet) is given by:
this 2nd cool result will be in class discussion on Tuesday
Wednesday, May 5, 2010
5/5 Scribe Post
Today we started with a warm up involving vectors. The first question was to find the component form, magnitude, and direction angle for vector AB and CD, with given points A(1,1) B(4,-1) C(-5,3) D(-2,1) .
The component form of both the vectors was <3,-2> and the magnitude was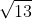
. To find the direction angle you create an axis with the initial point as the vertex. The direction angle is then measured counter clock wise. The direction angle is then,
, so the two vectors AB and CD are equal. This means that two vectors with the same component form are equal to each other.
Mr. O'Brien showed us the formula to find the component form:
Terminal Point - Initial Point. After this warm up problem we went over problem 59 from the homework. We found out that the component form can be found by
, usin> where u was 7/2 for problem 59.
The second warm up question: given u = <2,1> and v = <-1,4>
a. find 3u
b. Graph u and 3u on Geogebra, What do you notice?
c. Repeat a. and b. for u + v
d. Repeat a. and b. for u-v
For this problem we discovered that vector addition is done "tip to tail". So when vector u, vector v and vector u+v are combined they form a triangle. When a vector is multiplied by a number, it is a called a "Scalar multiplication" and it lengthens or shortens the vector.
ex. <3,4> to make a unit vector in the same direction:
Quiz:
After we completed the warm up we discussed the upcoming quizes and tests and decided to review the warm up at the end of class. Next we reviewed the quiz we took last class. Mr. Obrien showed us how to solve problem 1 on the quiz using a calculator only, but wanted to make sure that we could do this problem without a calculator using the sum and difference identity. To solve problem 1 you need to use the sum and difference formulas, then cancel and simply the equation. For problem 2 from the quiz Mr. Obrien recommended that we draw the triangles to start this type of problem. Problems 1 and 2 could both appear on a non-calculator section of a test. Problem 3 you needed to use factoring then an identity to simplify the expression. On problem 4 you needed to remember that there were two answers,
. Problems 5 involved using the Area of a triangle formula, A = 1/2 b x h or for this certain problem, A = 1/2 cbsinA. For problems 6 and 7 most people didn't have problems using the double angle formulas and the Law of Sines. The last problem, #8 gave people more trouble. It is important to use the correct fundamental identites.
The component form of both the vectors was <3,-2> and the magnitude was
Mr. O'Brien showed us the formula to find the component form:
Terminal Point - Initial Point. After this warm up problem we went over problem 59 from the homework. We found out that the component form can be found by
The second warm up question: given u = <2,1> and v = <-1,4>
a. find 3u
b. Graph u and 3u on Geogebra, What do you notice?
c. Repeat a. and b. for u + v
d. Repeat a. and b. for u-v
For this problem we discovered that vector addition is done "tip to tail". So when vector u, vector v and vector u+v are combined they form a triangle. When a vector is multiplied by a number, it is a called a "Scalar multiplication" and it lengthens or shortens the vector.
ex. <3,4> to make a unit vector in the same direction:
Quiz:
After we completed the warm up we discussed the upcoming quizes and tests and decided to review the warm up at the end of class. Next we reviewed the quiz we took last class. Mr. Obrien showed us how to solve problem 1 on the quiz using a calculator only, but wanted to make sure that we could do this problem without a calculator using the sum and difference identity. To solve problem 1 you need to use the sum and difference formulas, then cancel and simply the equation. For problem 2 from the quiz Mr. Obrien recommended that we draw the triangles to start this type of problem. Problems 1 and 2 could both appear on a non-calculator section of a test. Problem 3 you needed to use factoring then an identity to simplify the expression. On problem 4 you needed to remember that there were two answers,
Monday, May 3, 2010
Today we started with a homework quiz.
Then we proved why
We used Pythagorean theorem for the right triangle:
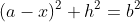
and we got that: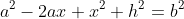
Then we used Pythagorean theorem for the left triangle:
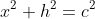
also we used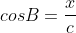
to get 
Then we substituted everything from the left triangle in the equation we got for the right triangle. So the final equation is:
It works with SSS and SAS.
The next part of the unit were vectors.
In math the vector is a segment with direction, also called directed line segment: 
The first point of the segment is called initial point (A), and the last point is called terminal point (B). a, b are components of the vector -
The length is sometimes referred to as magnitude,
Using Pythagorean theorem we could write it as:
The angle of the vector, θ is called direction angle.
examples:
1)Find the component form for a vector with initial point (-2,4) and terminal point (3,1).
The answer is <5,>
2)Find the component form for
and θ=45º
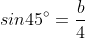, so 
, so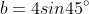 
The answer is
The rest of the class we went over hw.
Then we proved why
We used Pythagorean theorem for the right triangle:
and we got that:
Then we used Pythagorean theorem for the left triangle:
also we used
Then we substituted everything from the left triangle in the equation we got for the right triangle. So the final equation is:
It works with SSS and SAS.
The next part of the unit were vectors.
In math the vector is a segment with direction, also called directed line segment: The first point of the segment is called initial point (A), and the last point is called terminal point (B). a, b are components of the vector -
The length is sometimes referred to as magnitude,
Using Pythagorean theorem we could write it as:
The angle of the vector, θ is called direction angle.
examples:
1)Find the component form for a vector with initial point (-2,4) and terminal point (3,1).
The answer is <5,>
2)Find the component form for
The answer is
The rest of the class we went over hw.
Subscribe to:
Posts (Atom)
