At the beginning of class people had questions with the homework problems at the end of the assignment using the sum of the first n terms of any arithmetic sequence formula, #67, 69, 71, 85. We started with the warm-up which was doing the half-sheet of arithmetic sequences and series which was passed out to us last class. Mr. Obrien explained how make a table with arithmetic sequences to find the common difference. The graph of a arithmetic sequence has a linear graph, y = mx + b. He also reminded us to always check our answers for n by simply testing it.
Mr. Obrien showed how to solve the nth term without using the formulas, which was much quicker. For example:

,

, 9d +
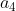
=

, 9d + 16 = 43, 9d = 27, d = 3. So instead of using formulas you can find
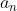
without them.
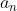
= 3n + 4. Because 3 is the difference so it is the nth term, then since you know
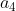
= 16, 4 x 3 = 12 + 4 = 16, so you found the nth term without using the formula.
We learned about Gauss's formula of finding how to find the sum of numbers 1 through 1000. So 1001 x 500 = 500500. The formula for this is:

.
Next students put up the answers to the questions from the homework that students had questions on. Mr. Obrien explained that there are three numbers between 10 and 12, 10, 11, 12. This sounds simply, but it is helpful to understand when doing problems such as #69 on the homework. Next he passed out a yellow half-sheet. We started by defining a geometric sequence:
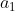

= r x
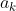
To finish class we filled in the formulas on the yellow sheet which we will use for tonights homework.
No comments:
Post a Comment